SSD (Single Shot MultiBox Detector) 是单阶段目标检测的主要框架之一，相比于Faster RCNN有明显的速度优势，相比于YOLO V1能够实现更高的检测精度。虽然被后面的YOLO 9000超越了，但是SSD的思想仍然值得学习。

相比于YOLO V1，SSD做了一下几个改变：

• SSD采用卷积来做检测，而不像YOLO V1在CNN之后接全连接层再做检测；
• 采用FPN结构(与YOLO V3类似)，输出多个尺度的feature map，应对不同大小的物体，而不像YOLO V1只有一种尺度的特征图；
• 借助Faster RCNN的Anchors思想，引入default boxes (prior boxes)。

由于我是先读的YOLO V3，再读的SSD，现在感觉YOLO V3借鉴了好多SSD的思想，再把这些东西做一定的优化然后放到YOLO的框架里面。

1. 网络结构

Fig 1. SSD网络结构

上图是SSD的整体结构，其采用VGG-16作为backbone，并在后面加了一些卷积层来踢去更多的特征以及做检测。SSD有两种网络结构，SSD300和SSD512分别对应$300 * 300$和$500 * 500$的输入大小。相比SSD300，SSD512的网络没有太大的差别，只是增加了一个卷积层，这里我们只讨论SSD300。从上图中可以看出，SSD只包含卷积层，没有全连接层，我们大致把它分为两个部分来帮助理解：Backbone, Auxiliary convolutions。

1.1 Backbone

Fig 2. VGG-16网络结构图

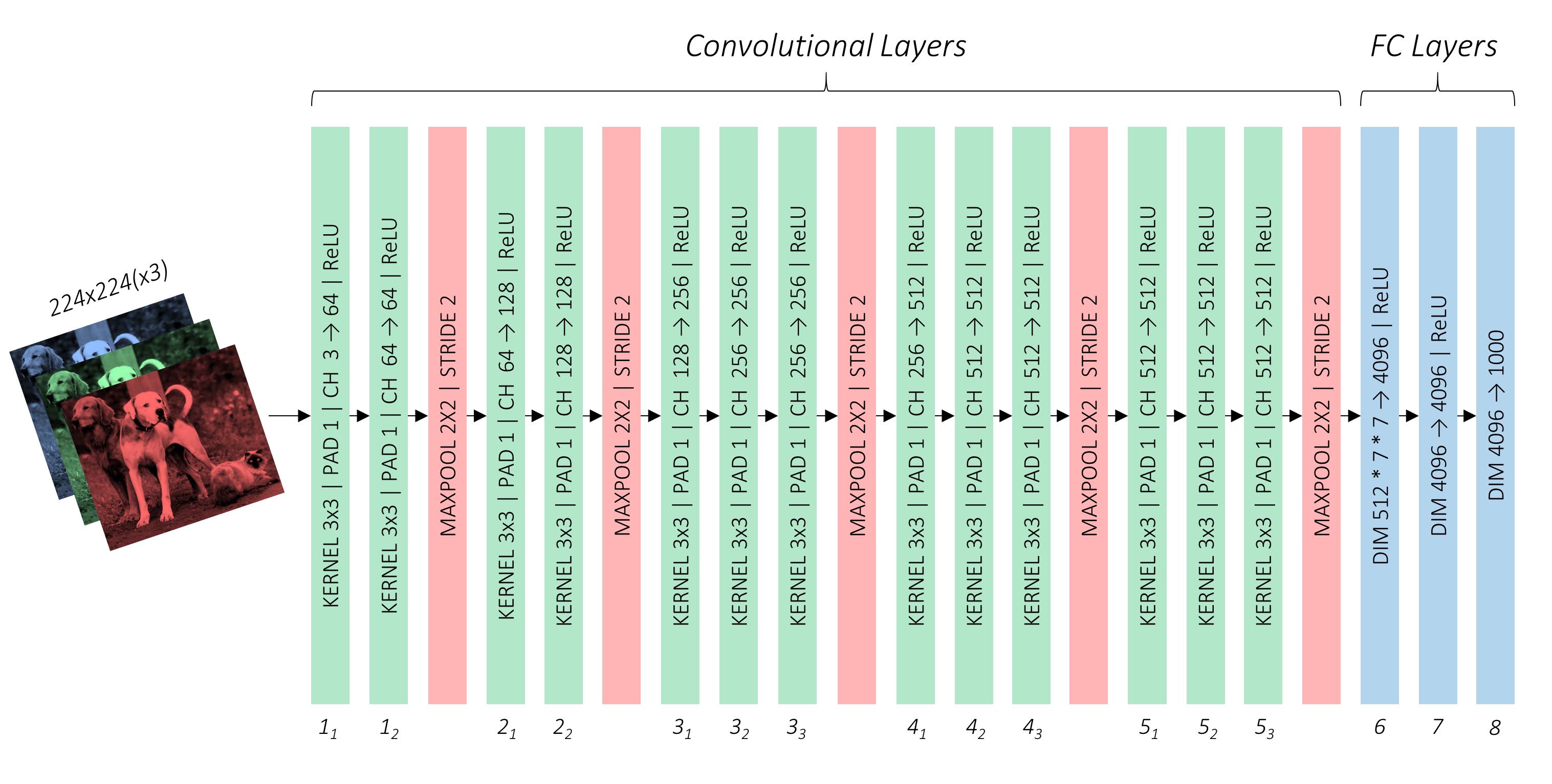
SSD的backbone采用在 ImageNet Large Scale Visual Recognition Competition(ILSVRC CLS-LOC) 数据集上与训练的VGG 16，但是做了一下几个改变：

• 分别把VGG 16的FC6和FC7变成$3*3$的卷积层Conv6和$1*1$的卷积层Conv7，关于为什么能够用卷积层替换券链接层以及如何做的 FC->Conv
• 把Pool5从$2\times 2 - s2$换成$3\times 3 -s1$，这样做的效果是不再使前一个卷积层的输出尺寸减半；
• 去掉了dropout layer 和 FC8；
• 采用$\grave{a}$ trous algorithm 。

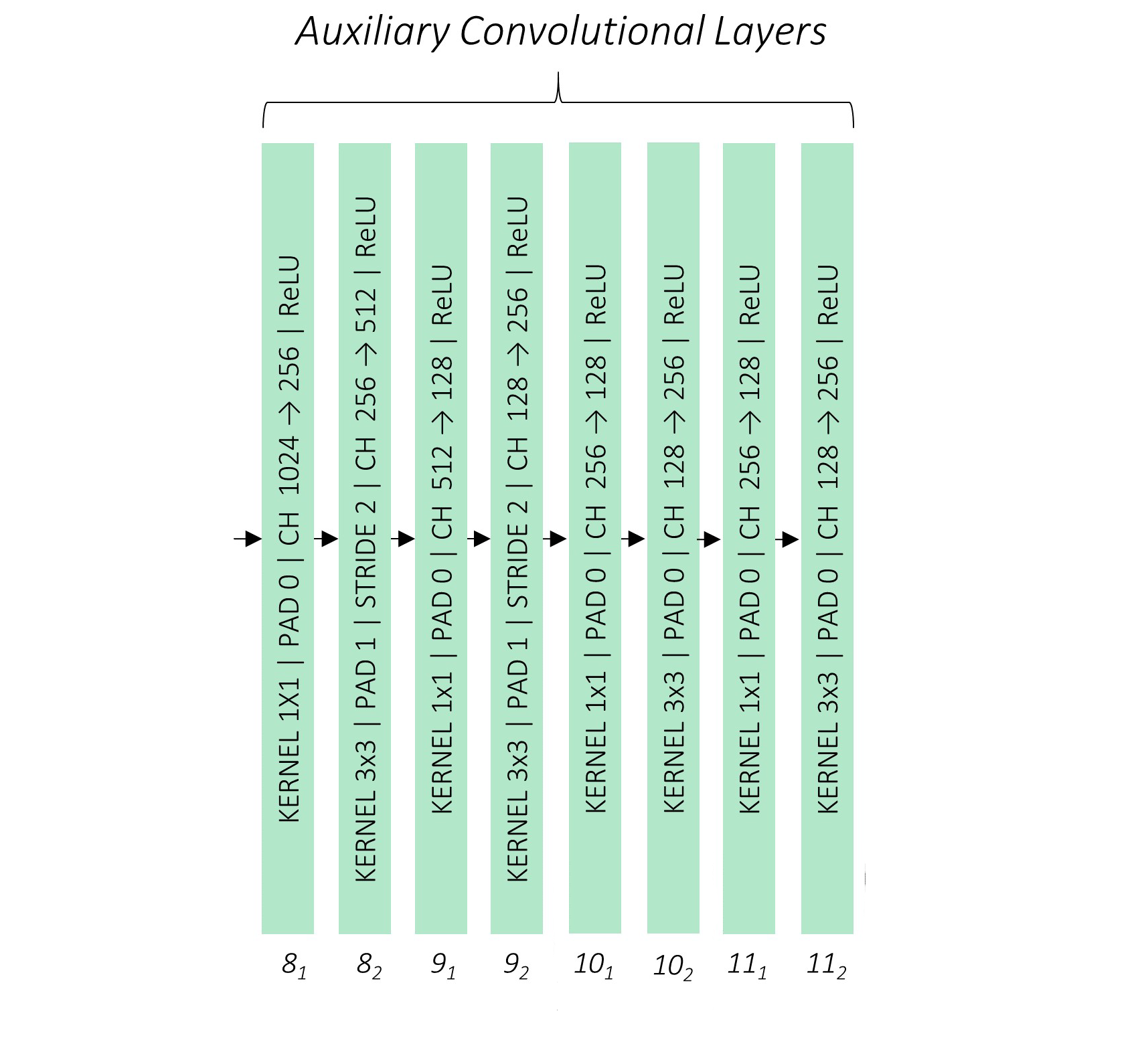
1.2 Auxiliary Convolutions

这部分是指在修改过后的VGG-16网络（即Conv7）后面再添加的卷积层，一共有4组，每一组包含2个卷积层，且不含池化层，通过卷积层的stride来调整特征图的大小。这样做是为了得到更多不同尺寸的特征图，提高检测能力。

Fig 3. Auxiliary Convolutions

2. 多尺度特征图

采用多尺度的特征图进行检测有助于提高检测题对物体大小的鲁棒性。较大的特征图有相对较小的感受野，对于小物体有较好的检测能力，相反，较小的特征图有较大的感受野，对于大物体有较好的检测能力。

Fig 4. Feature maps

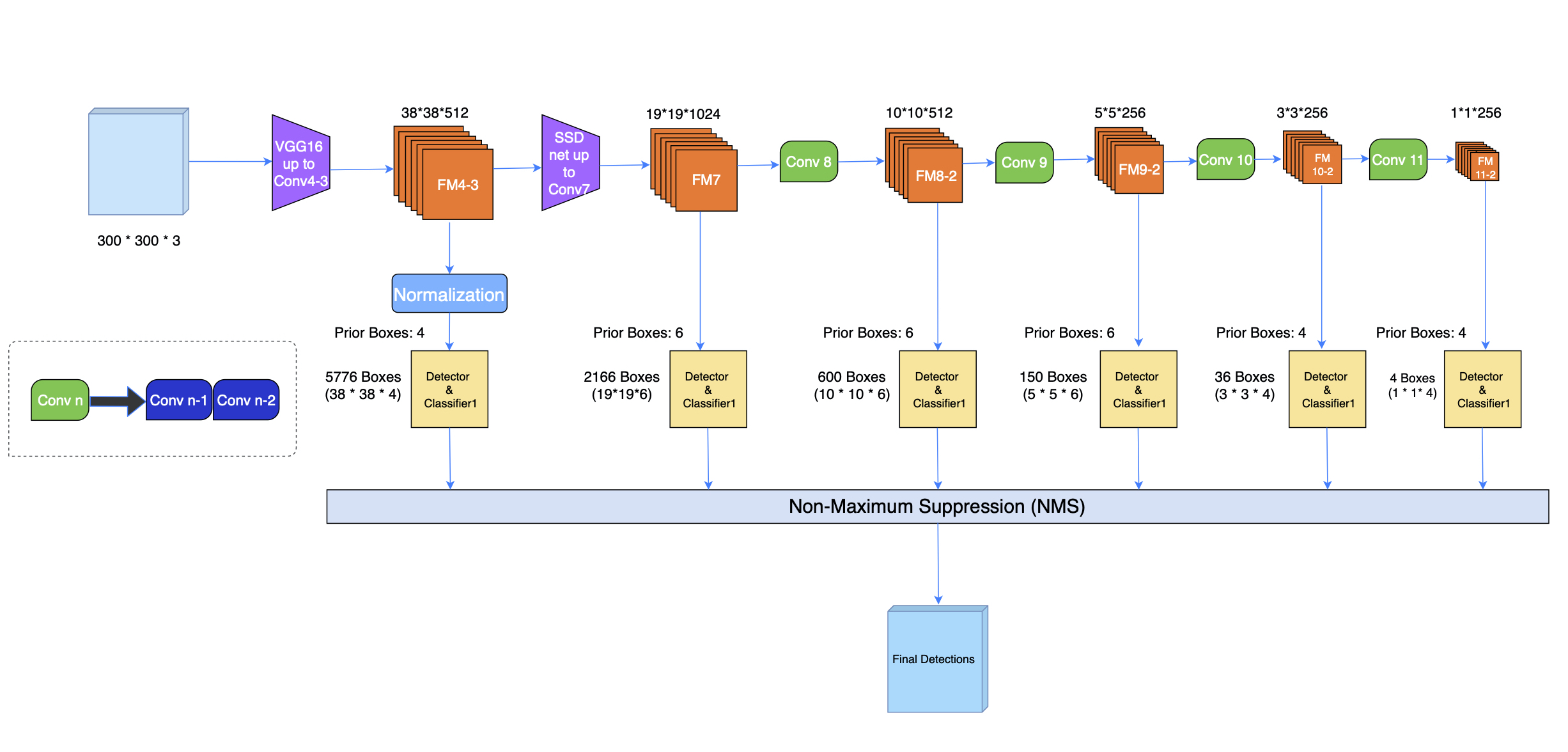
SSD一共生成了6种尺度的特征图，$38*38$, $19*19$, $10*10$, $5*5$, $3*3$, $1*1$，分别来自于Conv4-3, Conv7, Conv8-2, Conv9-2, Conv10-2和Conv11-2六个卷积层。关于为什么要使用多尺度特征映射，在YOLO V3的review里面已经提到过了。因为在CNN网络中，浅层次的卷积层对边缘信息更加感兴趣，可以获得更多的细节信息，而深层次的卷积层对浅层特征构成的复杂特征更为感兴趣，可以获得更多的语言特征。所以，在目标检测任务中，结合多种尺度的特征图作出预测，理论上可以提高检测器的表现。

3. 先验框

SSD借鉴了Faster RCNN Anchors的思想， 在每个特征图上引入不同数量，不同尺度（scale）和不同长宽比（aspect ratio）的先验框（Default/prior boxes ），而训练时预测的边界框（bounding boxes）是在先验框的基础上通过回归获得真实的目标位置。这些先验框是根据数据集里面的对象/目标的真实形状和大小手动设计的（YOLO V3是通过Kmeans聚类得到的），在把这些先验框放到特征图上的时候还需要考虑具体的位置、大小和数量。

3.1 Scales

如果一个先验框的尺度（大小）为s，也就是说先验框所覆盖的区域是一个s * s的正方形区域。对于第一个特征图（Conv4-3后面的特征图），论文中设置先验框的尺度比例为0.1，也就是图片尺寸的10%，其余特征图中先验框的大小按照公式逐渐增大，即特征图越小，先验框的尺度越大。

$$s_{k}=s_{min} + \frac{s_{max}-s_{min}}{m-1}(k-1), \quad k\in[1,m]$$

其中，$m=特征图数量-1$ ，即$m=5$，因为第一个特征图的尺度比例已经被指定了。$s_{min} = 0.2$，$s_{max}=0.9$，其余特征图的先验框的尺度比例从0.2到0.9均匀分布。在网上看到两种版本的尺度比例，查看SSD源码之后给出我自己理解的版本。对于输入为$300 * 300$的图片，第一个特征图的先验框的尺度为$300*0.1=30$。对于后面的特征图，先将$s_{min}$和 $s_{max}$ 都扩大100倍，然后根据公式 $\frac{s_{max}* 100-s_{min}*100}{m-1}$ 并进行向下取整得到增加的步长为17，然后便可得到后续几个先验框的尺度比例分别为：0.2，0.37，0.54，0.71，0.88，然后得到实际的大小分别为：60，111，162，213，264。

3.2 Aspect ratio

长宽比（aspect ratio）是先验框的另一个重要参数。作者在论文中设置了5种不同的长宽比$a_{r} \in \{1,2,3,\frac{1}{2}, \frac{1}{3}\}$。对于每个特定的长宽比和尺度（大小），根据公式可求出先验框具体的宽和高，注意，这里的$s_{k}$和$h_{k}$都是先验框实际的尺寸，而非尺寸比例。

$$w_{k}^{a}=s_{k}\sqrt{a_{r}} \quad h_{k}^{a}=s_{k}/\sqrt{a_{r}}$$

对于长宽比$a_{r}=1$尺度为$s_{k}$的先验框，还会额外的设置一个尺度$s_{k}^{‘}=\sqrt{s_{k}s_{k+1}}$且$a_{r}=1$的先验框，这样每个特征图就有两个长宽比为1但是不同尺寸的先验框。对于最后一个特征图的先验框，需要借助虚拟的尺寸来增加额外的先验框尺寸，$s_{m+1}=300 * 105/100=315$。所以对于每个特征图就会有6种先验框 $a_{r} \in \{1,2,3,\frac{1}{2}, \frac{1}{3},1^{‘}\}$，但是实际上，Conv4-3,Conv10-2, Conv11-2三层只使用了4种长宽比，没有使用床宽比为$3, \frac{1}{3}$的先验框。每个先验框的中心被设置在$(\frac{i+0.5}{|f_{k}|}, \frac{j+0.5}{|f_{k}|})$，$|f_{k}|$是第k个特征图的大小。

Table 1 SSD先验框设置

从表1可以看出，SSD一共需要设置8732个先验框。

3.3 先验框的设置

SSD中每个单元格的每个先验框都会输出一套独立的检测值，对应于一个边界框（bounding box）。这部分会在第四节详细介绍。网络真实的预测值其实是边界框$b=(b^{cx}, b^{cy}, b^{w}, b^{h})$相对于先验框$p=(p^{cx},p^{cy},p^{w},p^{h})$坐标和长宽的偏移量$l$，那么:

$$l^{cx}=\frac{b^{cx}-p^{cx}}{p^{w}} \quad l^{cy}=\frac{b^{cy}-p^{cy}}{p^{h}}\\ l^{w} = log(\frac{b^{w}}{p^{w}}) \quad l^{h} = log(\frac{b^{h}}{p^{h}})$$

称为边界框的编码（encode），在预测时，需要反过来即进行解码（decode），从预测值 $l$ 中得到边界框的真实位置：

$$b^{cx} = l^{cx}*p^{w} + p^{cx} \quad b^{cx} = l^{cy}*p^{h} + p^{cy}\\ b^{w} = e^{l^{w}}*p^{w} \quad b^{h} = e^{l^{h}}*p^{h}$$

3.5 先验框的匹配

3.5.1 Jaccard overlap

Jaccard Overlap 其实就是IoU（Intersection over Union），用来测量两个边框相互重叠的程度。

$$Jaccard \ Overlap = \frac{A\cap B}{A \cup B}$$

3.5.2 Matching

在YOLO中，真实目标（ground truth）的中心坐标落在哪个单元格内，那个单元格就负责预测这个真实目标。在SSD中，首先要确定输入图片中的GT与哪个先验框匹配，与之匹配的先验框所对应的边界框将负责预测它。SSD先验框的匹配主要有两点。

• 对于图片中的每个GT，首先找到与之Jaccard Overlap最大的先验框，与该先验框进行匹配，这样做可以保证图片中的每个GT都有一个先验框与之匹配。与GT匹配上的先验框被称为正样本，相反，如果一个先验框没有和任何一个GT进行匹配，则被认为与背景进行匹配，该先验框被称为负样本。在一张图片中，GT通常是很少的，如果只按照这个原则来进行匹配，这会产生很多负样本，不利于训练。
• 在完成第一个原则的匹配之后，在负样本中如果某个先验框与GT的Jaccard Overlap超过一个阈值（paper中设置的是0.5），那么这个先验框也被认为与这个GT相匹配。这意味着某个GT可以有多个先验框与之匹配，但是反过来却是不可以的。如果多个GT与一个先验框进行匹配，该先验框只会与Jaccard Overlap最大的那个GT进行匹配。第二个原则是基于第一个原则进行的，首先需要先保证每个GT都有一个先验框与之匹配，才能采取第二个原则来减少负样本。

所有正样本先验框都会被赋予GT的坐标和标签，在训练阶段负责该GT的预测。相反，负样本先验框将不会被赋予坐标，他们只会被赋予“背景”标签。

3.6 Visualize priors

sgrvinod给出了FM9-2种先验框的分布的例子。

Fig 5. SSD default boxes visualization

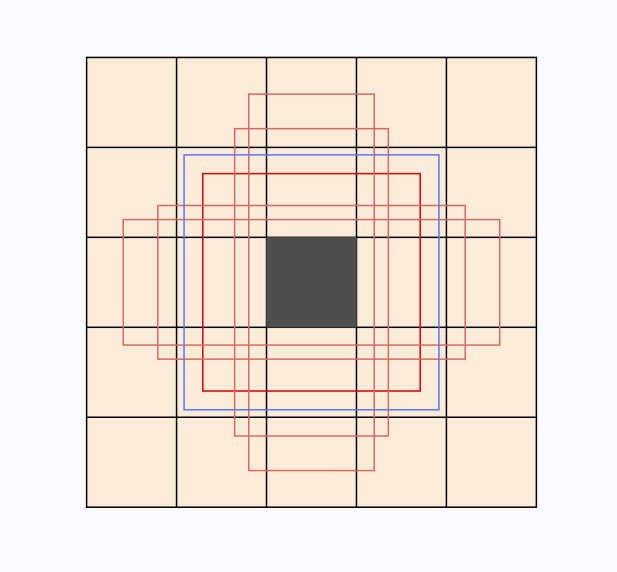
在$5*5$的特征图中的每个位置，都会有5个相同大小不同长宽比的先验框，图中红色的边框分别表示长宽比为$\{1，2，3，\frac{1}{2},\frac{1}{3}\}$的先验框，他们有相同的尺寸比例0.54，另外还会有一个长宽比为1，尺度比例为0.62的先验框。如果一个先验框覆盖的区域超过了特征图的范围，这个先验框将被去除。

4. Prediction convolutions

4.1 Predictions

在得到特征图之后，需要对特征图进行卷积才能得到检测结果，在每个特征图上，我们需要两个卷积核分别预测边界框的位置偏移和物体的类别。

• localization prediction：对于边界框的位置预测，在特征图的每个位置需要一个$3 \times 3 \times CH$的卷积核，$CH=4\times n_{k}$，$n_{k}$是该特征图中每个位置的先验框数量，4表示边界框的中心坐标和长宽相对于真实边框的偏差$(\hat{g}^{cx}, \hat{g}^{cy}, \hat{g}^{w}, \hat{g}^{h})$。
• class predication：对于类别预测，在特征图的每个位置需要一个$3\times3\times CH$的卷积核，其中$CH=c\times n_{k}$，c表示数据集包含的类别数量。

所以对于一个$m*n$的特征图，在每个位置需要$(c+4)* n_{k}$的卷积核，那么一共会产生$m*n*(n_{k}*(c+4))$个输出。由于每个先验框都会产生一个边界框，所以在一个$m*n$的特征图上会产生$m*n*n_{k}$个边界框。总的来说，SSD300会产生$(38 \times 38 \times 4)+(19 \times 19 \times 6)+(10 \times 10 \times 6)+(5 \times 5 \times 6)+(3 \times 3 \times 4)+(1 \times 1 \times 4) = 8732$ 个边界框。

4.2 Example

下面我们举个例子直观的理解一下表姐框的位置预测和类别预测。假设在Conv9-2特征图上预测3种类别，此时，$n_{k}=6$，$c=3$。

Fig 6. SSD prediction convolutions-(a)

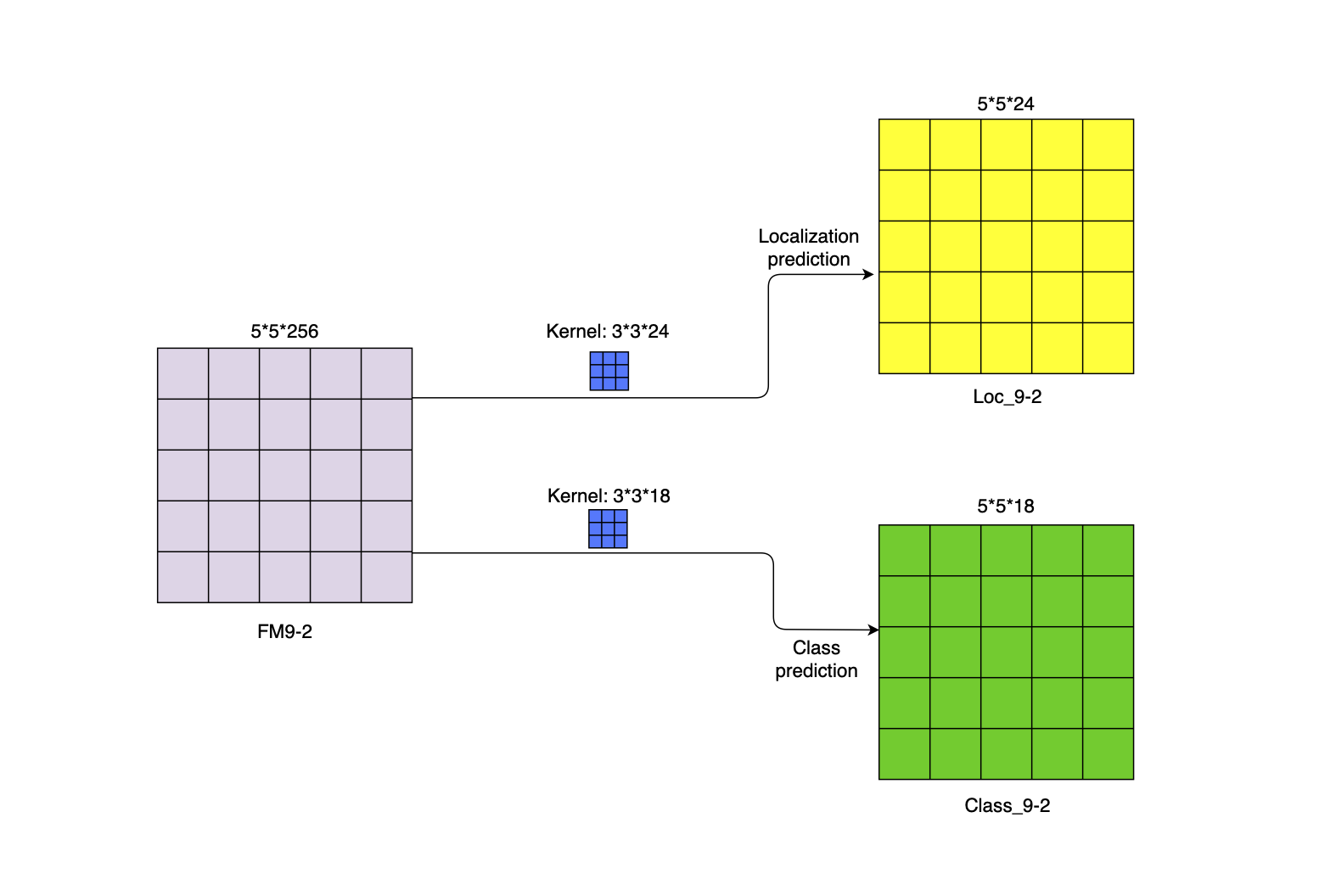
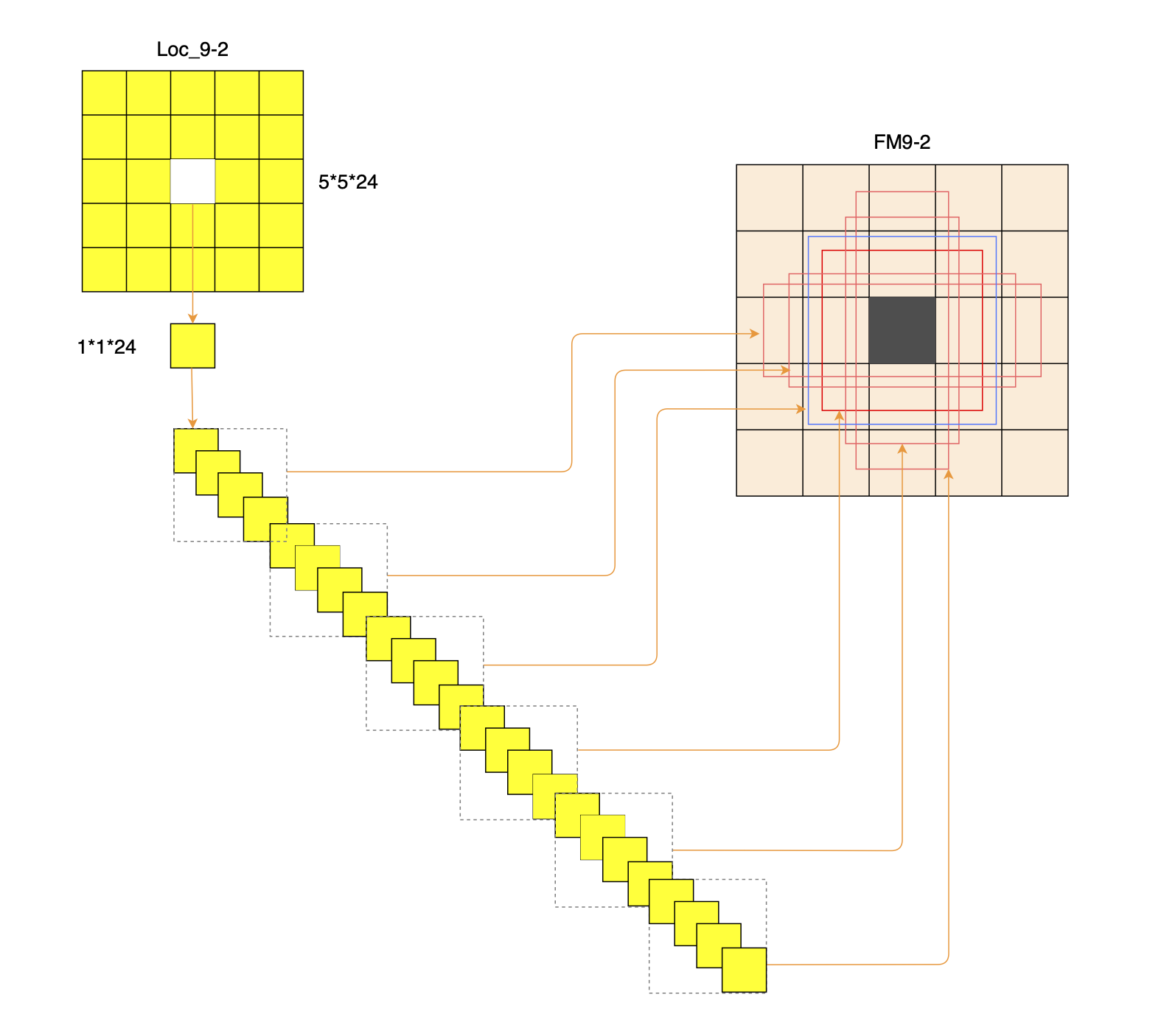
如图6所示，$5\times5$的特征图，经过$3\times3$的卷积核、padding之后，任然保持相同的尺度。但是我们真正感兴趣的是输出的维度，这里包含了特征图中每个位置/格子所产生的预测信息。下面我们把这写维度信息展开来一探究竟。

Fig 7. SSD prediction convolutions-(b)

如图7所示是把特征图中的一个单元格的对应的24个维度展开之后的事例。在Conv9-2的特征图中，每个格子会被分配6个先验框，每个先验框对于一个边界框，每个边界框会包含1组（4个）位置偏移信息。所以，在Conv9-2的特征图中的每个单元格中的每个边框对应24个维度中的4个，一共有6组位置偏移信息。

Fig 8. SSD prediction convolutions-(c)

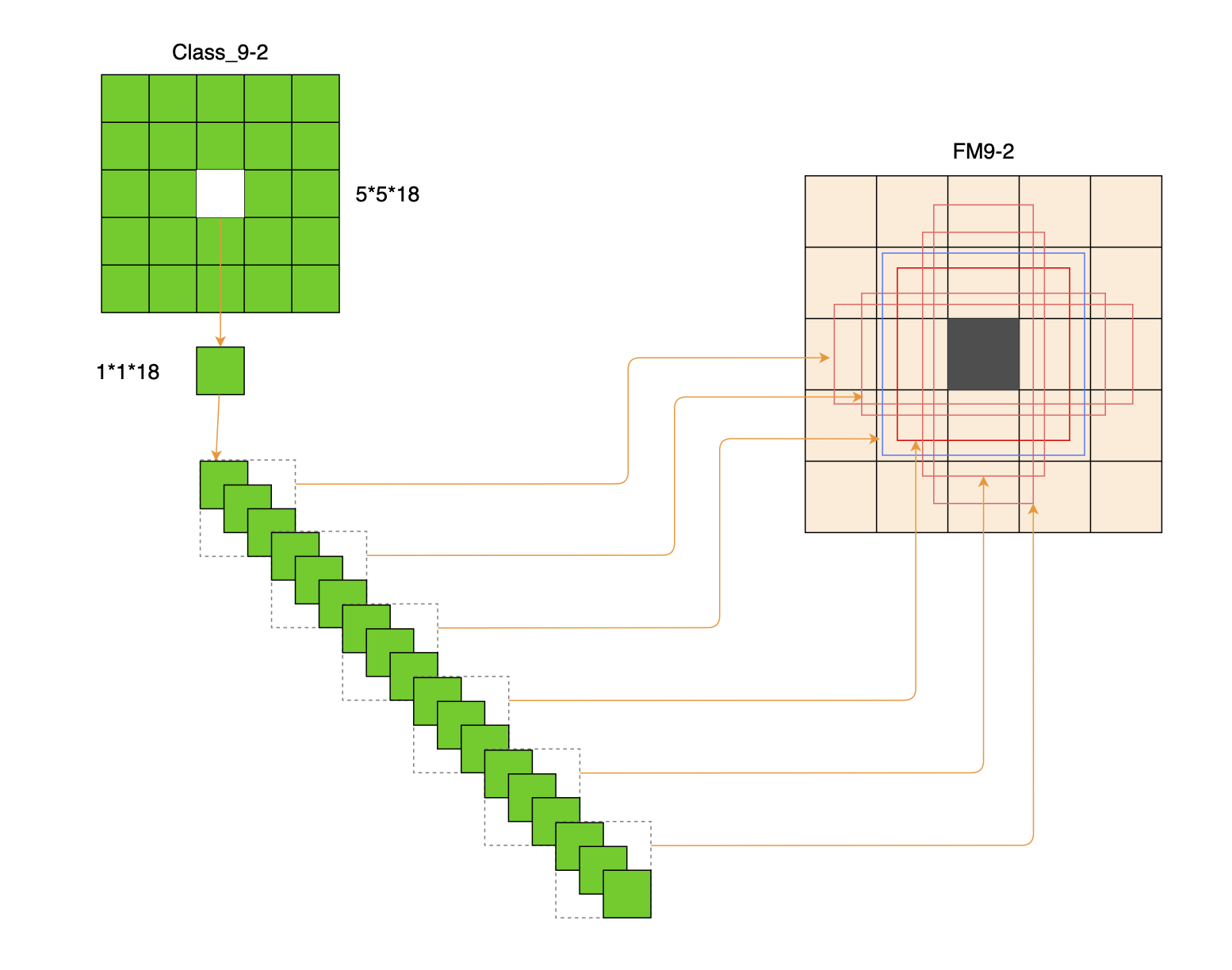
同样的，特征图中的每个单元格会对应一组（3个）类别信息。

把上面展开的维度重新整理一下可以得到下面更容易理解的版本。

Fig 9. SSD prediction convolutions-(d)

Fig 10. SSD prediction convolutions-(e)
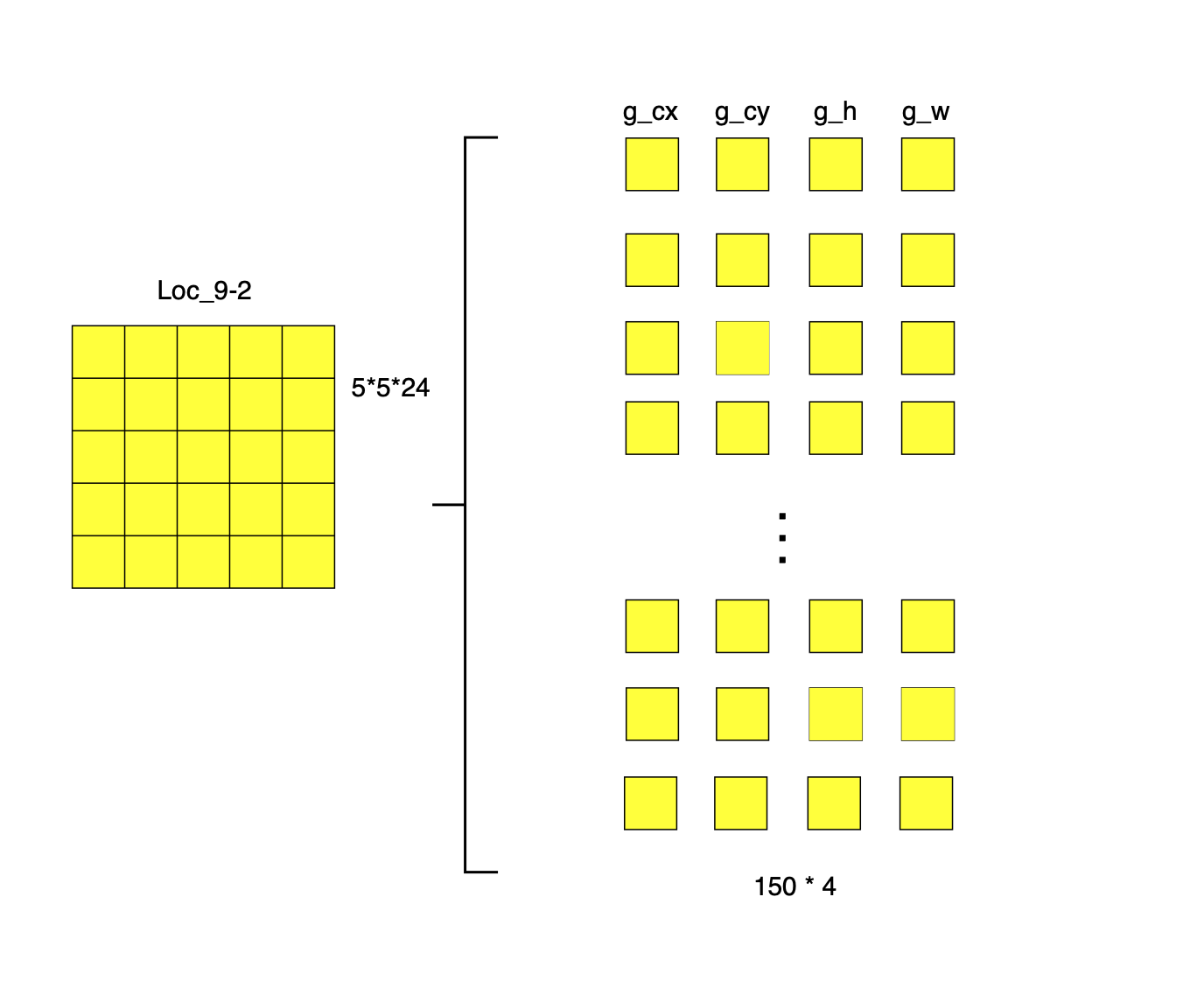
这样，在$5\times 5$的特征图中会产生150个边界框，这150个边界框会产生$150\times 4=600$个位置偏移预测和$150\times 3=450$个类别置信度。把同样的方法用到其余5个特征图上，SSD300对于3个类别的预测一共会产生$8732*4$的位置偏移预测和$8732*3$个类别置信度。

5. Loss functions

SSD 的损失函数是位置损失（Localization Loss）和置信度损失（Confidence Loss）的加权和。

$$L(x,c,l,g) = \frac{1}{N}(L_{conf}(x,c) + \alpha L_{loc}(x,l,g))$$

其中N是正样本的数量，如果$N=0$则设置损失为0。$x_{ij}^{p}\in\{0,1\}$是一个指示参数，当$x_{ij}^{p}=1$时表示第 $i$ 个先验框与第 $j$ 个GT匹配，并且该GT属于 $p$ 类。 $c$ 是类别置信度的预测值，$l$ 是先验框所对应的边界框的位置的预测值，$g$ 是GT的位置参数。对于位置损失，论文采用的是Smooth L1损失，通过回归得到关于先验边界框d的位置参数 $(cx,cy,w,h)$ 的偏移，定义如下：

$$L_{loc}(x,l,g)=\sum_{i\in Pos}^{N} \sum_{m\in \{cx,cy,w,h\}} x_{ij}^{k}*smooth_{L1}(l_{i}^{m}-\hat{g}_{j}^{m})\\ smooth_{L1}= \begin{cases} 0.5x^{2} & if \quad|x|<1\\ |x|-0.5 & otherwise \end{cases}\\ \hat{g}_{j}^{cx}=(g_{j}^{cx}-d_{i}^{cx})/d_{i}^{w} \quad \hat{g}_{j}^{cy}=(g_{j}^{cy}-d_{i}^{cy})/d_{i}^{h}\\ \hat{g}_{j}^{w}=log(\frac{g_{j}^{w}}{d_{i}^{w}}) \quad \hat{g}_{j}^{h}=log(\frac{g_{j}^{h}}{d_{i}^{h}})$$

对于类别置信度误差，采用Softmax损失，定义如下：

$$L_{conf}(x,c)=-\sum_{i\in Pos}^{N} x_{ij}^{p}*log(\hat{c}_{i}^{p}) - \sum_{i \in Neg}log(\hat{c}_{i}^{o})\\ where \qquad \hat{c}_{i}^{p}=\frac{exp(c_{i}^{p})}{\sum_{p}exp(c_{i}^{p})}$$

其中，$c_{i}^{p}$是第 $i$ 个正样本属于第 $p$ 类的置信度，$c_{i}^{0}$是第 $i$ 个负样本属于第0类（即背景）的置信度。权重 $\alpha$ 通过交叉验证得到为1。

6. Others

6.1 Data augmentation

在论文中作者通过实验说明了数据增强可以有效的提高SSD的性能。

• 随机调整照片的亮度、对比度、饱和度和色相；
• 缩小原始（zoom out）图像，缩小的图像必须是原始图像的1到4倍，这有助于让模型学习检测小尺寸的物体；
• 随机剪裁图片的某个区域，即放大图片（zoom in）的某个部分。裁剪区域的大小应该是原始图像的0.1到1倍，宽高比应该在0.5到2之间。如果真实对象（Ground Truth）的中心在剪裁区域中，那么我们将保留它重叠的部分。每个采样区域都会调整大小到 $300 *300$以符合模型的输入要求；
• 以50%的概率随机水平翻转图片；

6.2 Hard negative mining

在先验框匹配的时候提到，完成匹配后，大部分的先验框都会被认为是负样本，只有少数的先验框被认为是正样本，这样就会造成正负样本比例失衡。困难负样本挖掘（Hard Negative Mining）就是为了解决这个问题。论文中指出，预期使用所有的负样本，不如先按照置信度误差（confidence loss）进行降序排列（预测背景的置信度越小，误差越大）；然后再选择误差较大的前k个负样本进行训练，保证正负样本的比例接近 $1:3$。

6.3 $\grave{a}$ trous algorithm（空洞卷积）

在前文提到，SSD使用VGG-16作为backbone，但是把VGG-16的FC6和FC7换成了卷积层，由sgrvinod可知，对于一张大小为H，W并且有I个通道的图片，经过全链接层后有N个输出，相当于经过N个大小为（H，W，I）的卷积核。全连接层的参数维度为 N, H*W*I，卷积层的参数维度为 N,H,W,I。

• VGG-16的FC6层的输入维度为 7*7*512，输出为 4096 ，此时的参数维度是 4096, 7*7*512。相当于用 $4096$个 7*7*512 的卷积核进行运算，参数维度为 4096,7,7,512。
• VGG-16的FC7层的输入维度为 4096​ ，输出为 4096 ，参数维度为 4096,4096 。相当于使用 4096 个 1*1*4096 的卷积核进行运算，参数的维度为 4096,1,1,4096 。

但是，这样以来参数量极其庞大，计算成本太高。所以作者提出通过对转换后的卷积层的参数进行二次采样以减小卷积核的大小和数量。

• SSD Conv6采用 1024 个 3*3*512的卷积核；
• SSD Conv7采用1024 个 1*1*1024的卷积核。

这里就要用到$\grave{a}$ trous algorithm算法了，其在不增加参数量和模型复杂度的基础上扩大输出单元的感受野。对于Conv6，它从7*7 的卷积核采样到 3*3，为了维持相同的感受野，需要在3*3的卷积核上采用空洞卷积。虽然从7*7采样到3*3膨胀率（dilation rate）应该是3，但是作者实际采用的膨胀率却是6，这可能跟poiling-5的操作不再是对输入维度的减半有关。

参考

1. https://github.com/sgrvinod/a-PyTorch-Tutorial-to-Object-Detection/tree/783b39df5c69ce5b5c7fa1f4b70c68d368d90e68#training
2. https://blog.csdn.net/xiaohu2022/article/details/79833786#%E7%BD%91%E7%BB%9C%E7%BB%93%E6%9E%84
3. https://zhuanlan.zhihu.com/p/42159963
4. https://zhuanlan.zhihu.com/p/31427288
5. https://blog.csdn.net/thisiszdy/article/details/89576389